LayerDrop Regularisation + Knowledge Distillation?

Regularisation techniques such as Dropout is a powerful in preventing over-fitting of models during training. However, another benefit it confers is this- applying Dropout during model training has been shown to improve robustness to pruning. Leveraging this idea, the LayerDrop paper applies layer-wise Dropout to Transformers-based models such as the Transformer and RoBERTa, and was shown to greatly improve layer pruning. In this post, we explore how we can apply this technique in another way- training student model using Patient Knowledge Distillation, which could also confer benefits in layer-wise dropout during fine-tuning. We start by exploring the Dropout as a compression-robustness technique, then look briefly into the LayerDrop and Patient-KD papers. Then, we explore some experiments to quickly test the ideas, and finally conclude the findings.

Dropout as an Implicit Gating Mechanism For Continual Learning (arxiv, 2020)

This paper shows the role of Dropout on continual learning. In continual learning, where the goal of a network is to perform well as the domain changes as a function of time, the model should be able to generalize well. In generalization, the model should do well on in-domain tasks, where the training and test data are sampled from the same distribution (i.e. inductive transfer learning), and in out-domain tasks, where the training and test distributions differ (i.e. transductive). While SOTA NLP models today are effective due to their pre-training (with a language modeling-like objective), models like BERT require fine-tuning an additional classifier layer on top of the pre-trained BERT model (which thus acts as a feature extractor). The fine-tuning requirement limits the ability for effective zero-shot transfer, and thus limiting the out-domain generalization afforded by large-scale pre-training. This is the primary motivation for looking further into this paper.

The paper starts by introducing the stability-plasticity dilemma, where plasticity allows a neural network to incorporate new data in online learning, while stability prevents it from catastrophically forgetting what it has learnt. This paper shows how a DNN trained on SGD with Dropout increases its stability with a small performance cost, ameliorating a DNN trained on SGD without Dropout (with more catastrophic forgetting, as a result of having to learn new tasks with different domains). The stability–plasticity concept seems related to the Lottery Ticket (LT) hypothesis, where the latter states that a sub-network within a larger network is essentially responsible for the performance of the main network (and thus the rest can be pruned).

How are these two seemingly disparate ideas connected? Invoking the No Free Lunch theorem, my conjecture is that the LT Hypothesis allows us to select a sub-network that is effective for the current task, but likely does so at the expense of generalizing beyond the target domain, and thus trades network size for performance in a continual learning environment. On mobile devices, the performance of a DNN should be evaluated across its lifetime, and not only on inception, i.e. when the target domain is similar to the training domain. As such, we are motivated to procure compressed models that perform well in a continual learning enviroment. If Dropout and other regularisers (e.g. LayerDrop) does provide a good inductive bias towards out-domain generalization, it could form a better basis for training models that are eventually pruned or otherwise compressed. Evaluating compressed models on continual learning setups is also rather novel, from what I have seen; this could be something I could incorporate into my work.

LayerDrop

LayerDrop, where layers in a network are dropped randomly, improves a model’s ability to generalise and makes it more robust to pruning. Fan et al propose embedding the sparsity-inducing objective during training via a structured dropout mechanism termed LayerDrop. Akin to Dropout \cite{hinton2012improving} and DropConnect \cite{wan2013regularization}, the mechanism randomly drops layers of the original model during training, making it more robust to subsequent structured pruning of layer. Experiments show that pre-training RoBERTa with LayerDrop results in better performance on fine-tuned downstream NLP tasks (MNLI, MRPC, QNLI, SST-2) than BERT-Base and DistillBERT pruned to the same number of layers.

Knowledge Distillation

Training models with this regularization objective leads to better performance of pruned models. However, one problem remains: Pruning entire layers is still very destructive. Instead of pruning, can we have a knowledge distillation (KD) setup to learn a more compact representation from a LayerDrop-trained teacher?

Sun et al develop two strategies for knowledge distillation- Patient Knowledge Distilation (PKD)-Last, which learns from the last $k$ layers of the teacher network, and PKD-Skip, where the student network learns from every $k$ layer. The training objective is minimizing the mean square error loss of each layer in the student and teacher networks. This is in contast with the vanilla KD method that learns only from the last layer.

Instead of applying naive KD, where only the output logits of a teacher network is compared against the output logits of the student network, we can adopt a Patient-KD approach of mimicking every \(k^{th}\) level in the teacher network. However, figuring out which layers to patiently learn from is computationally intensive, as different layers have different functions in the NLP pipeline (lower levels does more POS tagging, dependency parsing, etc). How can we improve on this?

Experiments

Initially, I proposed to train a compressed student model by learning from a LayerDrop-trained teacher BERT model, using a Patient Knowledge Distillation framework. Unfortunately, I realized that the LayerDrop regularizer works well only if the model is trained during pre-training (and not fine-tuning), making it computationally too expensive for me to run these experiments. As a next pivot, I wanted to investigate how effective a Teacher model with layers removed would be under a patient KD objective. The results are summarized in the table and points below:

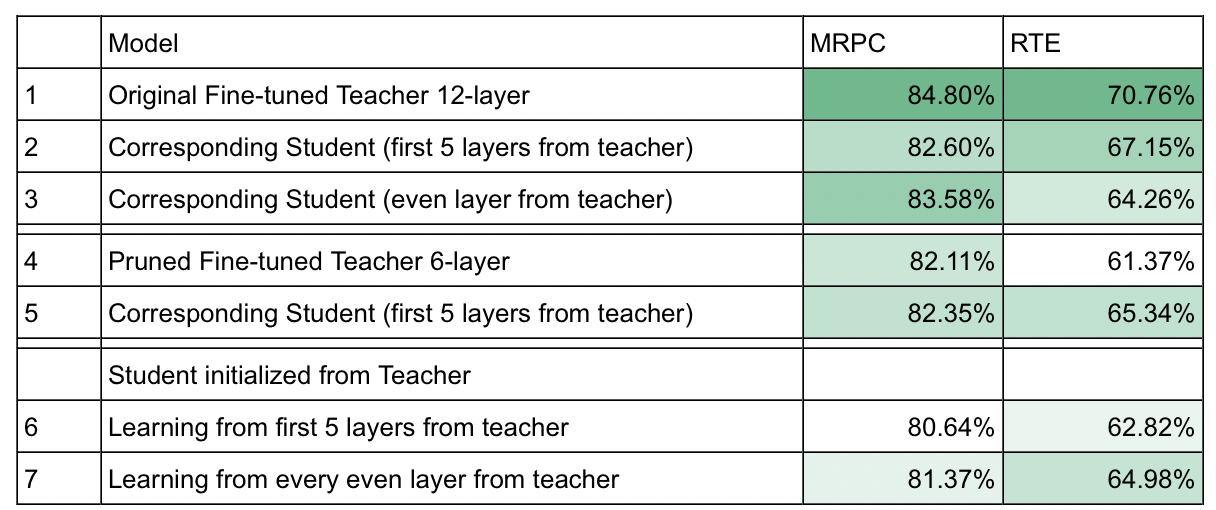
In these experiments, I tried 7 different configurations (denoted by # column) of BERT on two NLP tasks, MRPC & RTE, and report the dev set accuracy in % (with a green colour gradient, darker is better). Models #1 and #4 are teacher models, meaning they are pre-trained models that are fine-tuning on each individual classification task (with a cross-entropy loss objective). The other models are student models, which are trained with a Loss function that is the sum of the cross-entropy loss over the target labels, and the knowledge distillation loss (cross-entropy between the teacher’s and student’s output logits).

In #1, the original 12-layer model is fine-tuned on each task and serves as a teacher for #2 and #3. For #2 and #3, I trained a 6-layer student model to mimic the intermediate and final outputs from the teacher model (as per Patient Knowledge Distillation set-up). The difference between #2 and #3 is that for #2, layers 1,2,3,4,5,6 from the teacher (#1) are used to train the student model, while for #3, layers 2,4,6,8,10,12 are used. #2 and #3 are half the size of #1, and unfortunately knowledge distillation (KD) could not compress the model by 50% without significant loss.

In #4, I pruned layers 1,3,5,7,9,11 from the 12-layer model to produce a 6 layer model, then fine-tuned on each task. Naturally, #4 performs worse than #1, as it is half the size. Thus, we see that removing layers while providing only a few epochs for the model to train leads to a large performance drop. This is corroborated with (https://arxiv.org/pdf/2004.03844.pdf), showing that my initial idea of using LayerDrop during fine-tuning is limited. I note that an update from the LayerDrop authors show experiments where LayerDrop during fine-tuning doesn’t work well too; it only works really well as a regularisation during training over many epochs (so the model can recover).

In #5, the student is also a 6-layer BERT model, and it learns from all 6 layers of the teacher’s output. The weights of the student model are initialised as the BERT pre-trained weights, as with models #2 and #3. Comparing #5 and #4, we see that the student actually exceeds the performance of the teacher model. As the student is trained to both mimic the teacher as well as on the task, I believe that the slight performance gain of the student over the teacher is a result of the latter.

#6 and #7 was the idea I pivoted to, with hopes that KD can restore the damage done by pruning. #6 and #7 are student models that are trained from #1, but instead of loading the original weights from pre-trained BERT (as #2 and #3 did), it loads the weights from the pruned model (i.e. #4). In essence, I wanted to see if the pruned model #4 can learn from a full 12-layer teacher model, and tried the same layer permutations as #2 and #3. Unfortunately, training the pruned model is no better than directly using the pre-trained weights (comparing #6 with #2, #7 with #3). This corroborates with the Lottery Ticket Hypothesis (https://arxiv.org/abs/1803.03635; https://arxiv.org/abs/2005.00561), where training a pruned model is no better than directly training the initialised weights of the sparse architecture (in this case, a 6-layer model). I have shown that the KD set-up is no exception.

At this juncture, none of the results are that intriguing. To summarise, I showed that KD does beat the pruning for the same compression ratio, but ’stacking’ pruning and KD doesn’t work as well when directly training from a pruned network using its weights. Moving forward, I intend to look more into the Lottery Ticket Hypothesis line of research.

Conclusion

In this post, we explored an idea of combining the powerful regularization technique LayerDrop, with a Patient Knowledge Distillation set-up. Due to limitations in hardware, we started with a sanity check of checking to see this works on a fine-tuning set-up of the BERT model, instead of training BERT with the LayerDrop regularization from scratch. Unfortunately, the results are not that promising, suggesting that LayerDrop cannot be applied successfully in a fine-tuning setup.